Sucesión de Fibonacci: qué es, significados, fórmula, aplicaciones y ejemplos de la serie de Fibonacci en la vida real

La serie de Fibonacci, que fue creada a partir de la observación de la reproducción de los conejos, guarda muchísimos secretos que también se ocultan en algunas flores, en la concha de los nautilus y en el diseño de la Vía Láctea. Al observar la sucesión de Fibonacci se logra entender por qué Pitágoras hizo de los números su religión y por qué los matemáticos se apasionan por las fórmulas y los teoremas.  

La importancia de la teoría de Fibonacci  

La teoría de Fibonacci constituye un revolucionario descubrimiento que se remonta a la Edad Media, a través del cual se demuestran vínculos increíbles entre los números. A pesar de que anteriormente ya existía parte del conocimiento, mediante esta teoría se demostraron nuevas propiedades. Es muy importante conocer qué es la serie de Fibonacci para comprender el maravilloso universo de los números y por qué los matemáticos se apasionan tanto.

Quién fue el creador de los números Fibonacci

El nombre de quien reveló relaciones insólitas entre los números e ideó el denominado teorema de Fibonacci fue Leonardo de Pisa (1170-1240), conocido también como Leonardo Pisano. Fibonacci era un apodo, ya que a su padre lo llamaban Bonacci, que se puede traducir como bondadoso. Fibonacci viene a significar “figlio di Bonacci” (hijo de Bonacci).

Leonardo de Pisa vino al mundo en Italia, pero fue educado en Argelia debido a que su progenitor trabajaba como notario público en este país. Allí estudió Matemática y se familiarizó con el sistema numérico arábigo, muchísimo más avanzado que el romano ya que considera el cero y el valor de posición.

Los europeos no estaban al tanto de las posibilidades de cálculos que ofrecían los números arábigos, de lo cual se encargó Fibonacci en el año 1202 con la publicación de su libro Liber Abaci. En el mismo explicaba qué significa el cero matemáticamente, cómo un mismo número podría expresar unidades, decenas, centenas o unidades de mil, etc., y qué eran los números primos así como los principios de la divisibilidad.

Fibonacci es uno de los más destacados talentos en la historia de la Aritmética occidental, especialmente por ser el autor de la célebre frecuencia de Fibonacci, la cual está íntimamente relacionada con las formas y los eventos de la naturaleza.

Qué es la sucesión Fibonacci

Las series de Fibonacci son sucesiones de números que reflejan una interesantísima relación. Constan del conjunto ordenado de cifras cuyo valor se forma con la suma de los dos números anteriores, lo que da origen a otras relevantes inferencias matemáticas. Esta fórmula de la serie de Fibonacci también se distingue con los nombres de código secreto de la naturaleza y secuencia divina, ya que es posible encontrarla en los pétalos de las flores, las ramas de los árboles y los caparazones de ciertos moluscos. Por ende, desde siempre se ha buscado saber qué es Fibonacci con relación al mismísimo orden de nuestra realidad.

Origen de la sucesión de Fibonacci en la naturaleza

Una excelente forma de entender qué es la secuencia de Fibonacci y su vínculo con los eventos de la naturaleza es remontarse a su descubrimiento por parte de Leonardo de Pisa, lo cual sucedió cuando cavilaba sobre cómo se apareaban los conejos y trataba de predecir cuántos conejos habría a partir de una pareja según los meses transcurridos.

Como punto de partida para conocer qué es la serie Fibonacci aplicada a los conejos, hay que tener presente que esta especie alcanza su madurez reproductiva después de transcurrido un mes y posteriormente procrean otro par de conejos (ni más ni menos) con un período de gestación de aproximadamente 30 días. Y éste es uno de los mejores ejemplos para verificar la fórmula de Fibonacci en la vida real.

Sucede que: a) el primer mes sólo hay una pareja; b) en el segundo mes se reproducen y la coneja entra en período de gestación; c) el tercer mes nacen los conejitos y entonces hay dos parejas; d) la pareja adulta tiene otro par de conejos en el cuarto mes, pero los hijos no se reproducen todavía; e) cuando llega el quinto las dos parejas mayores vuelven a tener cría y hay dos conejitos más que nacieron en el cuarto mes pero que todavía no procrean.   

Esta tabla de Fibonacci se puede continuar hasta el infinito y en ella se observa que cada lectura es la suma de los dos valores anteriores. Para los primeros cinco meses los casos lucirían de la siguiente forma:

Mes	1	2	3	4	5
Pares de conejos	1	1	2	3	5

Algunas curiosidades interesantes  

Existen muchos datos relevantes en relación a los números de Fibonacci, relativos a distintos campos, de los cuales mencionamos algunos seguidamente.  

El cuerpo humano

En el cuerpo humano existe una proporción áurea, o muy cercana, al relacionar la altura total de la persona con la altura del ombligo. Igualmente en cuanto a la distancia que hay desde el codo a los dedos y a los hombros o desde las rodillas a las caderas y a los pies.

Las abejas

Igual que la sucesión de Fibonacci sirve para predecir los pares de conejos, también permite calcular el número de abejas machos y hembras de un panal y el número de hijos que nacerán a partir de un zángano.

La música

Los estudiosos de la música clásica han descubierto que existen proporciones áureas en la Sonata para piano n° 1 en Do Mayor de Mozart y en la Quinta Sinfonía de Beethoven. Estos cálculos se realizan en base al número de compases totales y los que contemplan cada uno de los movimientos.  

Los juegos de azar y la bolsa

En la actualidad se usa la secuencia de Fibonacci para predecir los movimientos de la bolsa y para apostar en los casinos, específicamente en la ruleta.

Aplicaciones de la sucesión de Fibonacci   

Para obtener el valor de cada posición según la fórmula de Fibonacci no es necesario calcular todos los valores previos, ya que existen ecuaciones que pueden ser aplicadas. Sin embargo, no es el objetivo entrar en profundidades acerca de funciones o polinomios, por lo que a continuación se señalan los primeros 30 números. Observándolos se puede apreciar en qué consiste la sucesión de Fibonacci, la cual, aparte de la relación ya mencionada entre sus valores, refleja algunas otras condiciones englobadas en la Ley de Fibonacci.

Primeros treinta números de Fibonacci

Tomando los números de las primeras treinta posiciones de la siguiente tabla se pueden hacer cálculos  interesantes para comprender qué es la sucesión de Fibonacci y cómo funciona. Además de que cada valor es la sumatoria de los dos anteriores, existen otros interesantes nexos que se explican a continuación del cuadro.

0	1	1	2	3	5	8	13	21	34
55	89	144	233	377	610	987	1.597	2.584	4.181
6.765	10.946	17.711	28.657	46.368	75.025	121.393	196.418	317.811	514.229

El número áureo  

Una de las propiedades de la fórmula de la sucesión de Fibonacci es que al dividir cualquier número entre el que está antes los valores van cambiando, pero llega el momento en que el cociente se estabiliza, lo cual sucede cuando la secuencia llega al número áureo. A los fines de comprender qué es el Fibonacci en este sentido, se recomienda hacer el cálculo para las primeras 30 cifras reflejadas en el cuadro anterior y se apreciará que esto sucede a partir del valor 17.711.  

El número áureo, también llamado número de oro o Phi es 1,61803399. Dicho valor está asociado con el equilibrio y la armonía, así como también se le asignan propiedades místicas. En el arte y la arquitectura se consideran obras de singular belleza las que tienen proporciones que dan como resultado el cociente indicado.  

Cálculo de algunos números de Fibonacci   

Una de las importantes características que nos ilustran acerca de qué es la secuencia Fibonacci se relaciona con el cálculo de los números de la tabla. Curiosamente, si sumamos los primeros cuatro números y le agregamos una unidad, obtenemos el valor del sexto número: 1+1+2+3+1 = 8. Igualmente, si sumamos los cinco primeros y le añadimos una unidad aparece el sexto término: 1+1+2+3+5+1 = 13. Y si sumamos los tres primeros números que tienen posiciones impares, obtenemos el sexto valor: 1+2+5 = 8.

Algunas propiedades de la sucesión de Fibonacci   

Otras de las cualidades de la serie de Fibonacci son que únicamente de cada tres números uno es par, de cada cuatro uno es múltiplo de tres, y de cada cinco uno es múltiplo de cinco. Por ejemplo, en la sucesión 3, 5, 8, 13, 21 se verifica que si tomamos los tres primeros sólo el 8 es par, si tomamos los cuatro primeros sólo el 3 contiene al número 3, y si consideramos los cinco mencionados sólo el cinco contiene al número 5.

Igualmente, si seleccionamos aleatoriamente a un grupo de valores más altos, por ejemplo la sucesión 55, 89, 144, 233, 377, se puede comprobar que sólo el 144 es par entre los tres primeros, así como también que 144 es el único divisible entre 3 tomando los primeros cuatro, y únicamente de los cinco 55 es múltiplo de 5.

Por otra parte, si seleccionamos un grupo de 10 números consecutivos, sin importar cuáles sean, tenemos que al sumarlos se obtiene siempre una cifra que siempre es múltiplo de 11, y la cantidad de veces que 11 está contenido en el resultado es igual al término que ocupa la posición siete de los escogidos. Asumamos la serie formada por 1+1+2+3+5+8+13+21+34+55 = 143. Si dividimos 143 entre 11 el resultado es 13, que es el séptimo número.

Todas estas propiedades también son fundamentales a la hora de entender qué es el Fibonacci y su relevancia dentro de las matemáticas.

Fibonacci en la ciencia y el arte

La secuencia de Fibonacci se observa tanto en la naturaleza como en el espacio. La representación gráfica de este fenómeno se conoce como la espiral de Fibonacci o el Caracol de Fibonacci y también ha sido utilizada como base de algunas creaciones artísticas.

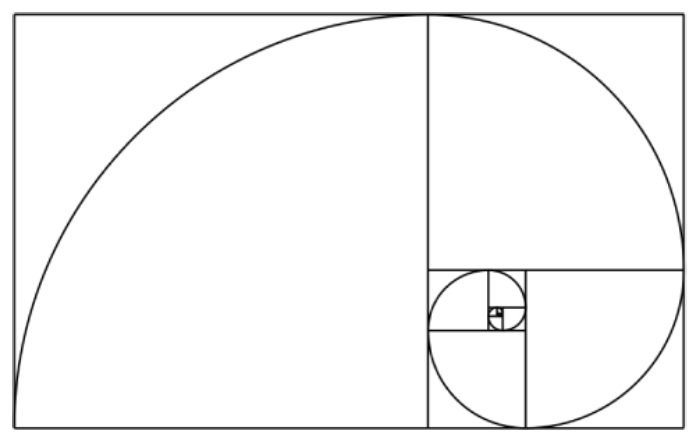
El significado del espiral de Fibonacci se traduce mediante una fórmula logarítmica, la cual representa un crecimiento relacionado con proporciones del número áureo y se expresa con una ecuación denominada Ecuación Polar.

Representaciones científicas

En la naturaleza se pueden admirar formaciones geométricas que se corresponden con la sucesión de Fibonacci y el número Phi tanto en las plantas como en los animales y en algunas galaxias, lo cual se amplía a continuación.

Botánica

La sucesión de Fibonacci y su espiral se refleja en algunas flores, como por ejemplo en el girasol o la alcachofa, así como en la cáscara de la piña.

Malacología

En la ciencia que estudia los moluscos también interviene la fórmula de Fibonacci y su caracol. La concha del nautilus es uno de los mejores ejemplos en este campo.

Astronomía

En Astronomía, la espiral de Fibonacci se aplica a las galaxias en forma de espiral como es el caso de la Vía Láctea, la cual es casi simétrica.

Representaciones Artísticas

En cuanto al arte, es posible observar la sucesión de Fibonacci en la pintura, la escultura y la arquitectura.  

Pintura

Uno de los pintores más geniales que aplicó el caracol de Fibonacci fue Leonardo da Vinci. Sin embargo, en tiempos más recientes, también Salvador Dalí lo usó como base de sus creaciones, lo cual quiere decir que Fibonacci y su espiral no son cosas del pasado. Igualmente, la famosa pintura Las Meninas de Velázquez está concebida en base a secciones áureas delimitadas por la espiral.

Escultura

Tal y como sucede en el caso de la pintura, en la escultura también Fibonacci está vigente. Recientemente un escultor y catedrático de la Universidad de Stanford, llamado John Edmark, creó una sobresaliente serie de esculturas basadas en la secuencia de Fibonacci.

Arquitectura

Con la arquitectura sucede de la misma forma, siguiendo presente Fibonacci en el trabajo de algunos arquitectos. En la modernidad destaca especialmente Le Corbusier, quien en los años 40 del siglo pasado diseñó hermosas edificaciones basadas en la proporción áurea. 

En la arquitectura es donde mayormente se observa la presencia del número de oro. Todas las iglesias góticas reflejan proporciones áureas y curiosamente también se ha detectado en construcciones como la Puerta de Bagdad y la Gran Muralla China.

La fórmula Fibonacci en lo religioso y lo esotérico

El hallazgo de mayor impacto respecto a la serie de números del matemático Leonardo Pisano es lo relativo al número de oro, conocido por civilizaciones muy antiguas y que además forma parte de la cabalística. A continuación se mencionan algunos ejemplos de la sucesión de Fibonacci relacionados con lo esotérico y lo religioso.

La Pirámide de Keops

Aunque se discute su antigüedad y se cree que puede ser mayor a la establecida, se dice que la Gran Pirámide de Guiza, también llamada Pirámide de Keops por el faraón que ordenó su construcción, fue finalizada en el año 2570 a.C. Como es sabido, las pirámides eran estructuras religiosas, que simbolizaban la divinidad de los faraones. 

Esta pirámide, que es la más grande de Egipto y está considerada como una de las siete maravillas del planeta, fue la construcción más alta del mundo hasta el siglo XIV, cuando se elevó en 83 metros de altura la Catedral Lincoln de Inglaterra, de estilo gótico. Pero siguió siendo la edificación de piedra de mayor altitud hasta el siglo XIX, en el que se reformó la iglesia de San Nicolás de Hamburgo agregándosele una aguja de 147 metros.    

La Gran Pirámide tiene cuatro lados de 230 metros de longitud cada uno que forman la base. Por otra parte, la distancia desde el punto medio de cada lado hasta el vértice de la pirámide originalmente era de 186,07 metros. Al dividir esta altura entre la mitad de la longitud de los lados, que equivale a 115 metros, el resultado es el número Phi.

Los pitagóricos

La Escuela Pitagórica agrupaba a los más avanzados matemáticos de la época y tenía características de secta. Los alumnos eran vegetarianos, llevaban a cabo rituales de purificación y sólo los más avanzados podían ver al Maestro. Igualmente, debían mantener en absoluto secreto todos los estudios y descubrimientos que en la escuela se realizaban.

Para los pitagóricos el principio de todo eran los números. Cuentan que estos estudiosos descubrieron el número áureo y cayeron en crisis cuando se percataron de que no era un número natural ni racional.

Cada número tenía un significado particular, siendo el cinco el más perfecto ya que representaba la belleza y la armonía. Por tal motivo, el pentágono, que posteriormente fue símbolo de la alquimia y la cábala, identificaba a los pitagóricos. Y casualmente ésta es la figura de proporciones áureas por excelencia.

El misterioso Leonardo da Vinci  

Da Vinci es uno de los genios más enigmáticos de la historia y su vida sigue siendo investigada. Incluso hay quienes dicen que fue la reencarnación de un antiguo Maestro ascendido. A pesar de su escasa formación académica hizo los primeros bosquejos del automóvil, el helicóptero y los submarinos, y sus conocimientos anatómicos, productos de sus visitas a los hospitales para participar en la disección de cadáveres, era envidiable.

Se sabe que Leonardo realizó profundos estudios acerca del número Phi y se le atribuye el enunciado del término sectio áurea que se traduce como divina proporción. En todas sus pinturas está presente el número de oro, especialmente en su Hombre de Vitruvio donde aparecen sus propias anotaciones señalando las relaciones de proporción en base al mismo, que están presentes en el cuerpo humano.

Igualmente sucede con el rostro de la Mona Lisa, y en su cuadro La Última Cena en el que la mesa, las ventanas y la manera como están colocados Jesús y sus apóstoles responden al uso magistral de número áureo. Según los expertos, esta pintura representa una gran incógnita y en ella existen muchos mensajes velados acerca de la religión que aún no han podido ser interpretados cabalmente.

Imágenes relacionadas con la sucesión de Fibonacci  

A continuación se presentan algunas imágenes que ilustran los casos mencionados respecto a las aplicaciones de la sucesión de Fibonacci en la naturaleza o su utilización por parte del hombre. 

Flor de girasol

Las semillas que se encuentran dentro de la corona de la flor del girasol crecen en forma de espiral y reflejan las sucesiones de Fibonacci.

Concha de nautilus

La concha del nautilus es el modelo más perfecto de la espiral de Fibonacci que se puede apreciar.

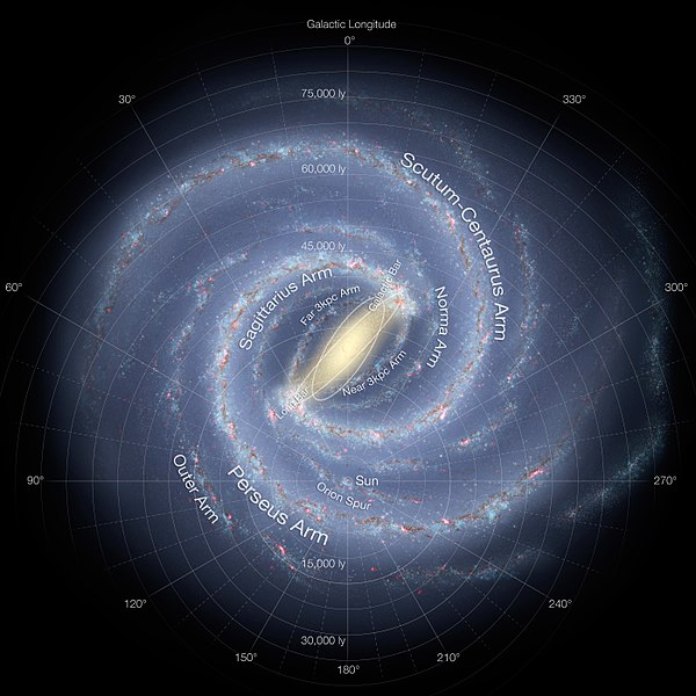
Vía Láctea

Nuestra galaxia tiene forma de espiral y una simetría casi perfecta que sigue el modelo de Fibonacci.

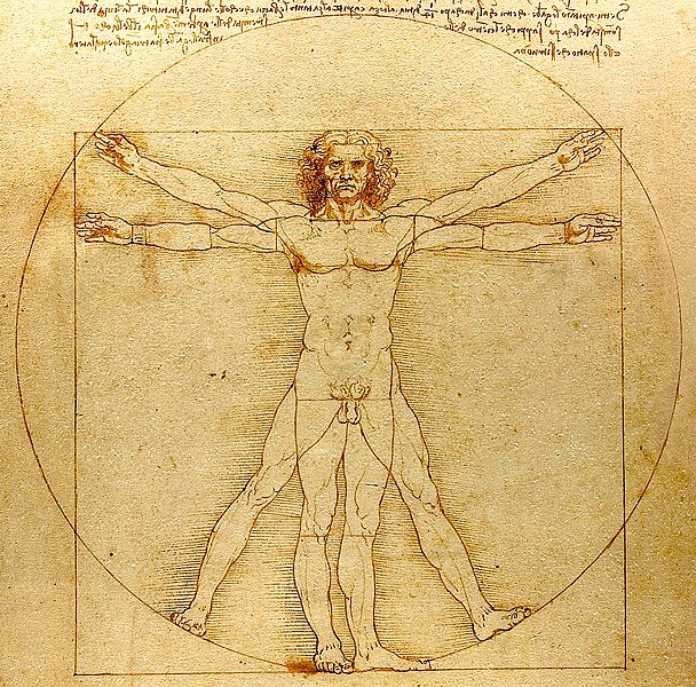
Hombre de Vitruvio

El Hombre de Vitruvio de Leonardo da Vinci representa la perfección del cuerpo humano de acuerdo al número áureo.

Analizar la sucesión de Fibonacci es un estímulo espiritual en cuanto a que, si existe tanta perfección, la vida debe de tener algún sentido. La serie de Fibonacci, por otra parte, nos enseña que los números son misteriosos y contienen muchos grandes secretos de la naturaleza y del cosmos.